지식추적에 적용한 셀프 어텐션(Self Attention)
Transformer가 등장하면서 셀프 어텐션(Self Attention)은 시퀀스 데이터를 처리하기 위한 필수적 요소로 사용되고 있는데요. 대표적으로 문장과 같은 자연어가 이에 해당합니다. 지식 추적 (Knowledge Tracing) 에서도 학생의 풀이 이력이라는 시퀀스 데이터를 다루게 됩니다. 그렇기 때문에 이 셀프 어텐션을 지식추적에 활용한 모델 구조가 연구되었고, 그 중 "A Self-Attentive model for Knowledge Tracing(SAKT)" 논문이 대표적입니다. 본 글에서는 SAKT를 통해 지식추적에 셀프어텐션을 어떻게 적용했는 지 상세히 살펴보고, 파이토치 코드를 통해서도 이해하고자 합니다.
A Self-Attentive model for Knowledge Tracing, SAKT 논문을 기반으로 논문의 기호 및 수식은 그대로 사용하되 제 언어와 그림으로 재구성 했습니다. 그 과정에서 생략되거나 추가된 설명이 있을 수 있으며 오류가 있다면 언제든 의견 부탁드립니다 😊
1. Model Input
Knowledge Tracing 모델의 입력은 학생의 풀이이력이 들어가게 됩니다. 문제 풀이이력은 시간 순차적으로 쌓이는 시퀀스 데이터이기 때문에, 1 ~ t 까지의 문제 풀이이력을 입력하면, 모델은 2 ~ t+1 의 정오답을 예측해내면 됩니다. (1 ~ t 시점의 문제 풀이이력 입력 => t + 1 시점의 문제 정오답 예측)
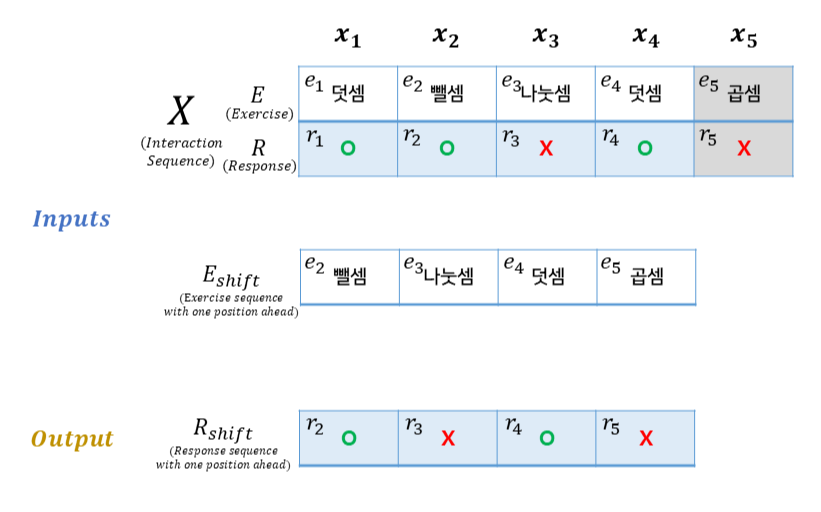
SAKT 의 Input(입력)은 크게 두가지로 분류되는데, 첫번째로 X(Interaction Sequence) 입니다. 학생의 문제풀이이력에 해당하며, 문제 풀이이력, 즉 상호작용을 논문에서는 Interaction 이라 표현하고 있습니다. 설명을 위해 "덧셈", "뺄셈", "곱셈", "나눗셈" 총 4가지의 개념에 대한 문제 여러개가 존재한다고 가정했으며, 문제는 Exercise, 정오답 여부는 Response 입니다.
첫번째 문제 ("덧셈" 개념의 문제에 해당, 맞음), 두번째 문제는 ("뺄셈" 개념의 문제에 해당, 맞음) ,.. 으로 이해할 수 있습니다. 해당 학생은 총 5문제를 풀었다고 가정했으며, Interaction Sequence 의 길이는 총 5라고 할 수 있습니다. 그런데, 보시다시피 5번째 Interaction(x_5)는 회색 처리 해두었는데요. 이 이유는 E_shift 에 있습니다. Exercise(문제) 시퀀스를 앞으로 한칸씩 당긴 것을 E_shift 라 표현했습니다. Knowledge Tracing 의 목적은 다음 문항의 학생의 정오답을 예측하는 것에 있으며, SAKT 에서도 이를 위해 t 시점에서의 문제풀이이력 뿐 아니라, t+1 시점의 문제 시퀀스를 함께 입력으로 넣어주어 다음 예측해야할 문제의 정보를 함께 입력해줍니다.
따라서 5문제를 풀었지만 한칸 앞으로 당긴 sequence가 함께 필요하므로 입력에는 길이가 4인 sequence들이 들어가게 되는 것입니다.
Output은 E_shift, 즉 다음 문항들의 실제 정오답이 들어갑니다. 모델이 예측한 문제 정오답 확률과의 비교를 통해 학습이 진행될 수 있습니다.
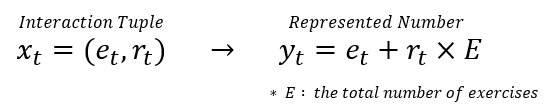
모델의 Input과 Output을 알았으니, 이것들이 실제로 모델에 어떤 모습으로 들어가는 지 알아보겠습니다. 그림2는 논문에 나와있는 Interaction Tuple을 Number로 나타내는 식입니다. 식으로만 보면 이해가 쉽지 않으니 예제에 그림으로 적용해보겠습니다.

예제에서의 개념, 즉 Exercise에서 표현될 수 있는 종류는 덧셈, 뺄셈, 곱셈, 나눗셈 총 4가지 였습니다. 이를 순서대로 0, 1, 2, 3 으로 표현할 수 있습니다. 또, 이에 대해 나올 수 있는 정오답은 틀림 맞음 총 2가지 이므로, 으 또한 0과 1 로 표현될 수 있습니다.

예제에서, x_1에 해당하는 ("덧셈" 문제, 맞음) 이라는 Interaction 은 어떻게 표현할 수 있을까요? 그림 2 에서 보았던 식에 넣어보면 됩니다. 덧셈은 숫자 0에 해당했고, 맞았다는 것은 1로 표현할 수 있다고 했습니다. 그럼 해당 Interaction은 0 + 1 * 4 즉 0으로 표현될 수 있습니다. x_2은 어떨까요? 뺄셈은 1, 맞았다는 것은 1이므로, 1 + 1 * 4 즉 5로 표현할 수 있겠네요.
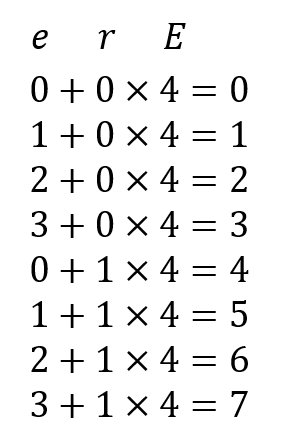
따라서, 개념의 개수가 4개 Interaction 에서는 그림 5와 같이 계산하여 총 8개의 숫자로 표현될 수 있습니다. 논문에서는 이렇게 Interaction sequence를 숫자로 표현한 것을 sequence y 로 칭했으며, 예제에서 sequence y는 (4, 5, 3, 4) 가 되는 것입니다.
2. Embedding
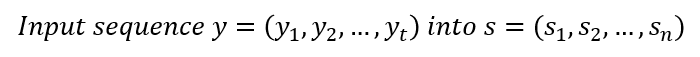
Interaction sequence를 숫자로 바꿔주었다면, 이를 임베딩하는 과정이 필요합니다. 그 전에 논문에서 s 라고 표현하는 sequence로 한번 더 변환해주는 과정이 필요한데요. 만약 시퀀스 최대 길이를 100(n) 으로 설정했다면, s 의 길이는 100이 되고 y의 길이는 총 4였으므로, 나머지 96개 자리에 -1 등의 수로 패딩해주게 됩니다. 아래 그림에서 좀 더 자세히 살펴보겠습니다.
1) Interaction embedding
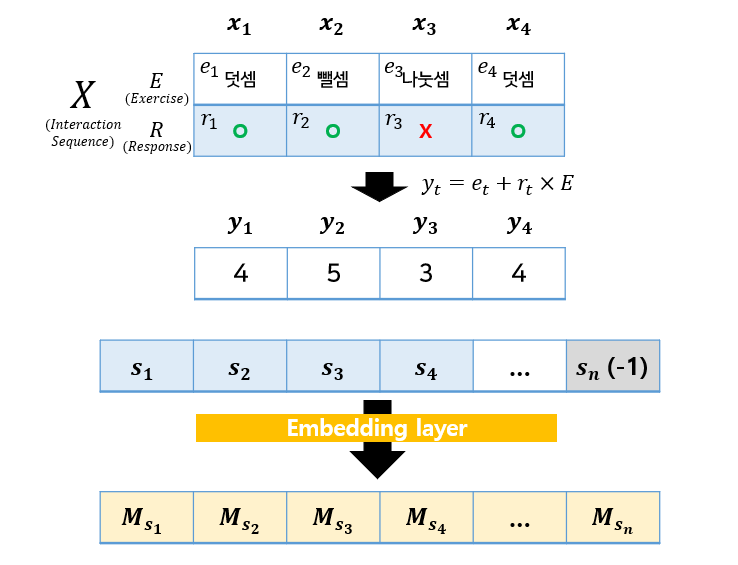
Interaction을 sequence y 로 바꾸는 과정까지 진행했었습니다. 위 예제에서는 y = (4, 5, 3, 4)로 표현되었고, 이를 최대 시퀀스 길이에 맞춰준 sequence s 로 변환해줍니다. 그림에 표현한 것처럼, s_1 ~ s_4는 y_1 ~ y_4와 같도록 그대로 넣어주고, 이 후 위치들에는 -1로 padding 작업을 진행해줍니다.
이제 이 sequence s 를 임베딩 해주면 되는데요. Embedding Layer 에 통과시켜주면 s1 은 길이가 d인 임베딩 벡터 M_s1 이 됩니다. 이 임베딩 벡터들은 이후 어텐션 계산에 사용되게 됩니다.
2) Exercise embedding
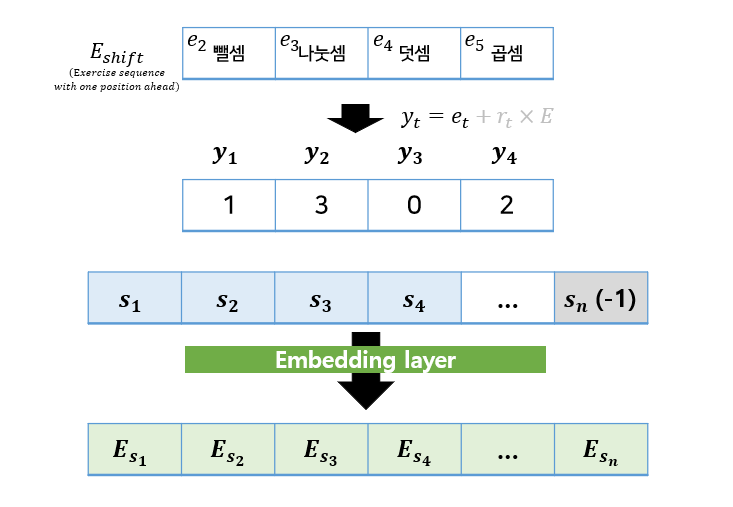
모델의 입력이 크게 2개로 나뉜다고 했었는데요, 1 ~ t-1 의 문제 풀이이력(Interaction)과 2 ~ t 의 문제 (Exercise) 였습니다. 이 E_shift 또한 숫자로 바꾸어 주는 작업이 필요하며, 이때도 그림2와 같은 식에 넣어주면 되는데요. 다만 Exercise는 response(정오답) 정보가 없으므로 y = e 로 표현해주기만 하면 됩니다. (+r * E 생략) 따라서 Exercise Pool에서만 가져와 y = (1, 3, 0, 2) 로 표현되었네요.
Interaction Embedding 과 동일한 과정으로 sequence s 를 만들어주었다면, 임베딩 해주면됩니다. 이 때의 Embedding Layer는 Interaction Embedding Layer 와 다른 임베딩 레이어임을 생각해주어야 합니다. 이 임베딩 벡터들또한 이후 어텐션 계산에 사용되게 됩니다.
3) Positional encoding
https://www.blossominkyung.com/deeplearning/transfomer-positional-encoding
트랜스포머(Transformer) 파헤치기—1. Positional Encoding
트랜스포머 Transformer Attention is All You Need Postional Encoding
www.blossominkyung.com
🏋️♂️ 저는 Positional encoding 을 이해하는 데 위 글의 도움을 99% 받았습니다! 직관적이고 이해하기 쉽게 잘 정리된 글이니 참고하시면 좋을 듯 합니다.
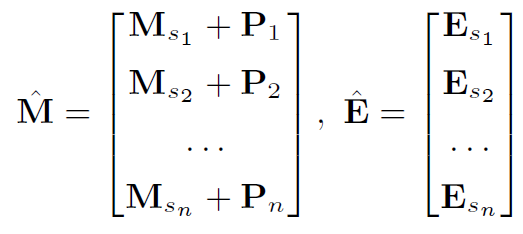
SAKT 에서는, 두가지 임베딩 벡터를 사용하게 되는데요. 그림 9 에서 M_hat 이라고 표현된 Embedded Interaction input matrix 와, E_hat이라 표현된 Embedded Exercise Matrix 입니다. 바로 위에서 M와 E 임베딩 벡터들은 어떤과정으로 생성되는 지 과정을 살펴보았었습니다. M_hat에 추가된 것은, 문제풀이결과(Interaction)을 임베딩한 M Matrix 에 Positional Encoding(포지셔널 인코딩)입니다. 이는, 문제풀이이력을 표현하기 위해 (개념+정오답) 뿐 아니라, 풀이이력 시퀀스에서의 위치까지 표현하겠다는 의미입니다.
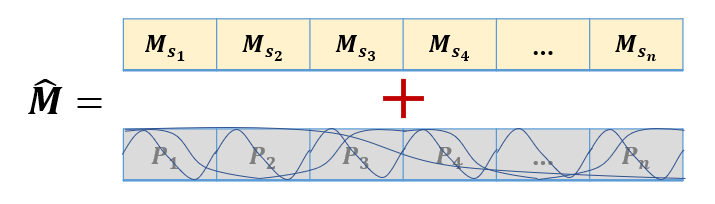
Positional Encoding의 구현 방식을 표현하기 위해 사인 함수와 코사인함수인 주기함수를 그림에 표현하려 노력했습니다. ㅎㅎ 아무튼 M_s1, M_s2,... M_sn 이라 표현된 문제풀이이력에다가, 각 풀이이력의 위치를 표현한 Positional Encoding 을 Concatenation 하여 최종적으로 문제풀이시퀀스의 위치정보까지 담은 M_hat을 만들어냈습니다.

그림 8에서 설명했던 문제풀이이력에서 (개념-Exercise)정보가 담긴 임베딩벡터로 이루어진 임베딩 행렬, E_hat 입니다.

다시 한번 더 정리한 그림 12 입니다. M_hat은 문제풀이이력의 (개념+정오답) 정보를 임베딩했던 M과, 위치정보를 나타내는 Positional Encoding인 P의 합(Concat) 입니다. E_hat은 문제풀이이력에서 (개념) 정보를 임베딩한 E 입니다.
3. Self-attention
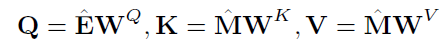
지금까지 살펴봤던 임베딩 행렬을 사용할 차례입니다. 바로 Self-Attention (셀프 어텐션) 연산을 진행하는 것인데요. SAKT 에서 셀프어텐션은 그림 13에 표현된 Equation 을 따릅니다.
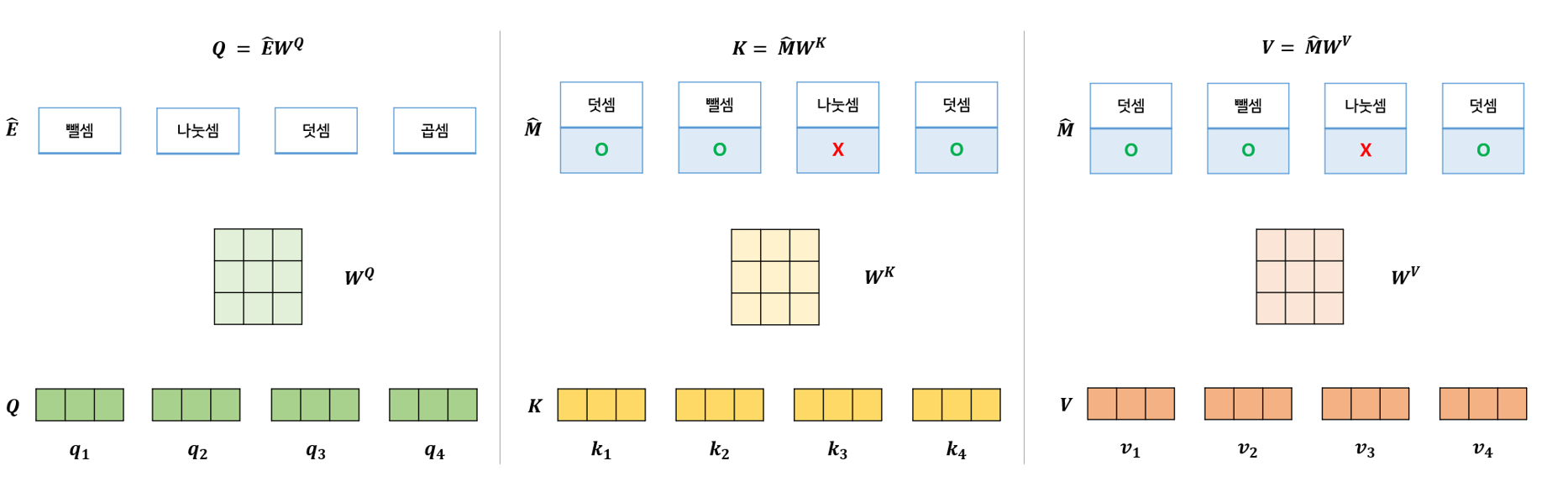
그림 13의 Equation을 그림으로 풀어서 표현했습니다. 공통적인 구조는 Query, Key, Value 모두 문제풀이이력으로 부터 얻은 임베딩 벡터에, 가중치 행렬을 곱해 Query, Key, Value 벡터들을 구하는 것입니다.
Query를 예로 먼저 설명해보겠습니다. 다음시점의 문항들의 시퀀스 (E_shift) 들을 임베딩 했던 E_hat 을 사용해주게 됩니다. 뺄셈 이라는 개념을 임베딩 했고, 해당 임베딩 벡터의 크기가 (1 * 3) 이라고 가정하겠습니다. 이와 곱해져야 하는 가중치 행렬의 크기는 (d * d), 예시에서는 dimenstion을 3으로 정해서 (3 * 3) 이 됩니다. (논문에서 d*d 크기의 가중치 행렬을 사용합니다.) 따라서 하나의 개념 벡터로 부터 q_1 이라는 (1 * 3) 크기의 벡터가 탄생하게 됩니다. 이 작업을 시퀀스 내의 모든 개념에 대해 진행하고, 이 벡터들이 모여 Q 행렬이 만들어 집니다.
Key, Value 는 동일한 임베딩 벡터로 부터 시작되는데요. Interaction 임베딩 벡터인 M_hat에 가중치 행렬이 곱해져 K와 V 행렬을 만들게 됩니다. 마찬가지로, Interaction 임베딩 벡터의 크기가 각각 (1 * 3) 이라 가정하면, (3 * 3) 크기의 가중치 행렬과 곱해져, 첫번째 Interaction(덧셈, O) 으로부터 (1 * 3)크기의 k_1이, 두번째 Interaction(뺄셈, O) 으로부터 (1 * 3)크기의 k_2 벡터가 만들어 집니다. 이 벡터들이 모여 K행렬이 되고, v_1, ... v_n 벡터들이 모여 V 행렬이 되는 것입니다.
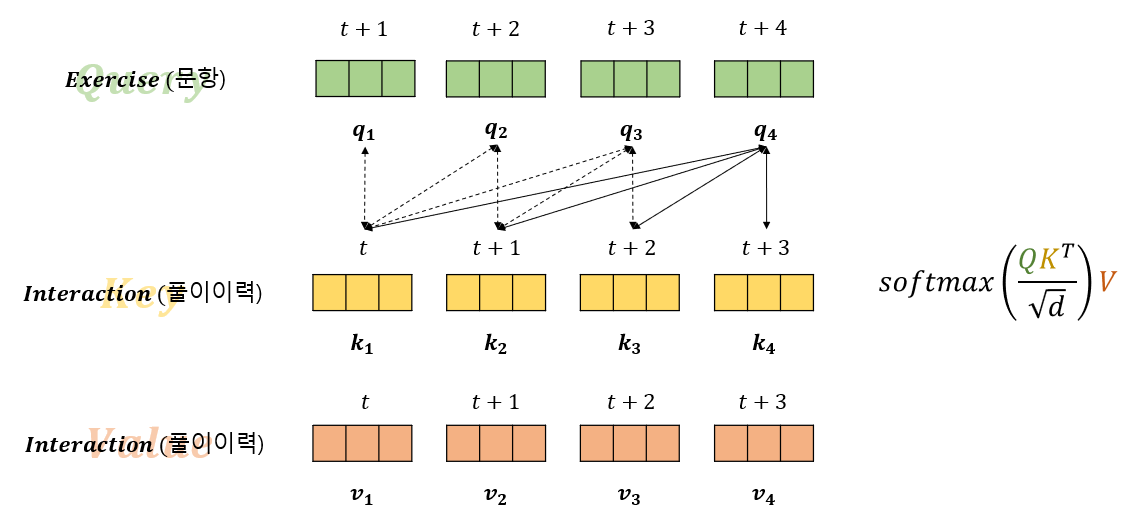
그렇게 Q, K, V 를 구했다면, 그림 15의 우측에 적힌 공식에 따라 Attention Score 를 구하게 됩니다. Knowledge Tracing에서는 이전 이력들을 통해 다음 문항의 정오답을 예측하게 된다고 했는데요. SAKT 에서 이를 구현하기 위해 Query로 다음 시점에 풀이한 문항들을 날리게 되고, 이와 계산되는 Key와 Value들은 모두 이전 이력들이 됩니다. 그림 15와 함께 살펴보겠습니다.
📍만약 t+4 시점에 풀이한 문항의 정오답을 예측한다고 하면, t+3 이전 시점들의 풀이이력 만을 사용해 연관성을 파악해야 할 것입니다. 그래서 q_4 는 k1, k2, k3, k4 즉 t ~ t+3까지의 풀이이력을 나타내는 Key 와 내적되어 Attention Score가 계산됩니다. 또한, q_2의 경우에는 k_1와 k_2의 관계만 구하게 되는것이죠. SAKT 논문에서는 아래와 같이 표현하고 있습니다.
In our model, we should consider only first t interactions when predicting the result of the (t + 1)st exercise.
There-fore, for a query Q_i, the keys K_j such that j > i should not be considered.
We use, causality layer to mask the weights learned from a future interaction key.
우리 모델에서는 (t + 1)번째 Exercise의 결과를 예측할 때 첫 번째 t개의 Interaction만 고려해야 합니다.
따라서 쿼리 Qi에 대해 j > i와 같은 키 Kj는 고려되어서는 안 됩니다.
우리는 미래의 Interaction Key로부터 학습된 가중치를 마스크하기 위해 인과성 레이어를 사용합니다.
다시 말해서, 학생의 이전 풀이이력들과, 현재 예측하고자 하는 문항의 개념과의 연관성을 Attention 연산으로 파악해서, 이후 예측에 사용하게 됩니다. 마지막 줄에서, "미래의 Interaction 으로부터 학습된 가중치를 마스크" 한다는 것은 현재 예측하고자 하는 문항에 대한 정오답을 예측하기 위해 미래의 문제풀이이력은 반영하지 않겠다는 뜻이며, 이를 위해 모델에서는 MASK 한다는 의미입니다. 아래 그림을 보며 좀 더 직관적으로 이해할 수 있을 겁니다.
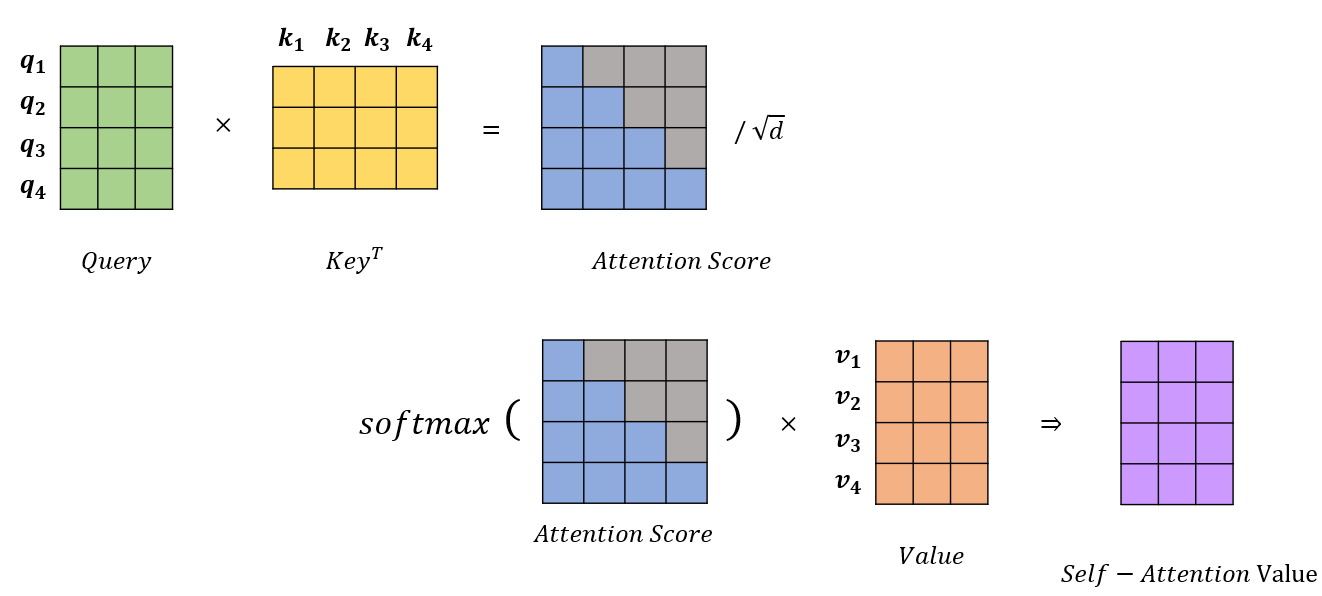
그림 16의 Attention Score에서 회색부분이 마스크된 부분입니다. q_1의 경우, k_1과의 내적만 진행하므로 계산된 Attention Score의 첫번째 행에는 첫번째 열만 계산되어 파란색 표시하였습니다. 즉 Attention Score의 (0,0) 자리는 q1 * k1 내적의 결과 값이 들어갑니다. q_2는 k_1과 k_2와만 내적되는데요. 그렇기 때문에 Attention Score의 (1,0) 자리는 q2 * k1내적의 결과 값, (1,1) 자리는 q2 * k2 내적의 결과값이 들어갑니다. 이렇게 모든 Query와 Key 행렬에 대해 내적을 완료했다면 그림 15에서 봤던 Attention 식에 따라 벡터 dimension인 3의 루트를 씌운 값으로 나눠줍니다. 이 값은 Softmax 함수에 들어가 0에서 1사이의 값으로 표현되어, q와 k와의 연관성을 나타냅니다.(1에 가까울 수록 관련도 높음) 마지막으로 이 값에 Value 행렬의 내적을 해 최종 Self-Attention Value가 구해집니다.
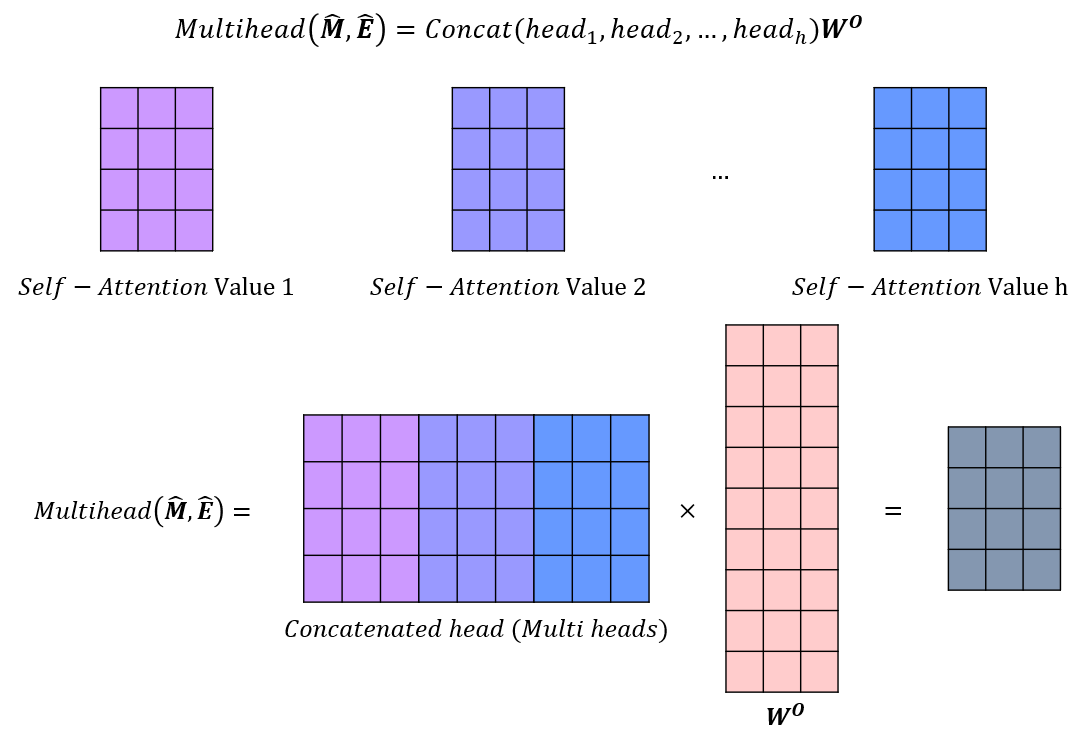
SAKT 논문에서는 Multi-head 어텐션으로 연결합니다. 앞서 구했던 Self - Attention Value들이 head라고 할 때, h 개의 head 를 Concatenation 하여 h*d 만큼의 row를 가지는 W 가중치와 곱해 완성됩니다.
4. Prediction
1) Feed Forward Network

Self Attention 연산에서 가중치를 부여했었고, 가중치의 최적값을 찾는 과정이 필요합니다. 이를 위해 멀티헤드 어텐션의 결과를 입력으로 넣어, Feed Forward Network를 통해 Attention에 활용한 가중치 행렬을 학습하게 됩니다. 그림 18에서 볼 수 있듯 논문에서는 Linear Regression 과 ReLU 활성화 함수로 연결해 학습을 진행해주었습니다.
2) Prediction Layer
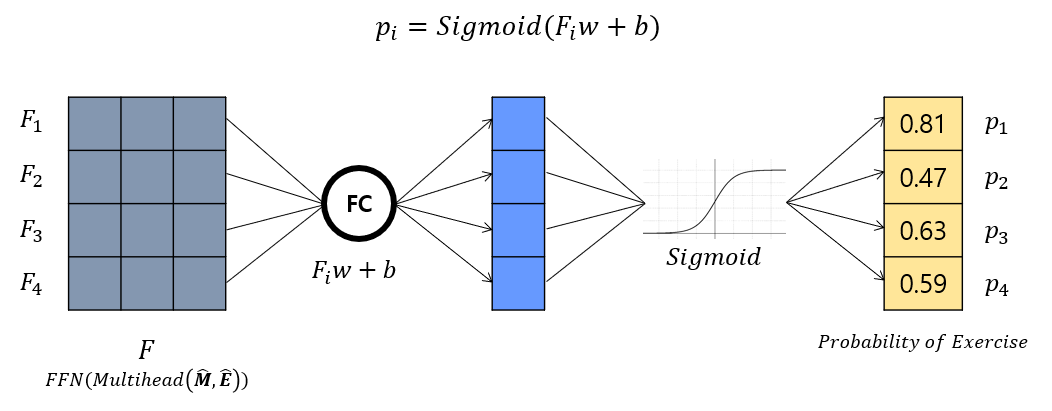
이제 거의 다왔습니다! 다음 문항(E_shift) 에 대한 정오답을 예측해내는 과정인데요. 그림 19 상단에 있는 p_i에 대한 수식이 SAKT 모델을 통해 도출할 수 있는 문항별 맞을 확률을 추출하는 식입니다. 해당 식을 아래와 같이 그림으로 표현해보았는데요. 위에서 저희는 FeedForward 과정을 통해 예측해야 하는 Exercise들의 어텐션 값을 뽑아냈었습니다. 그것을 F라고 했을 때, F 를 Fully Connected Network 를 통과시켜 주고, 도출된 값을 최종적으로 0 과 1사이의 값으로 출력하기 위해 Sigmoid 활성화 함수에 통과시켜주는 모습입니다.
📍다시 정리해보겠습니다. 제가 지금 계속 사용하고 있는 예제는 총 5개의 문항풀이이력을 통해, 다음 시점의 문항에 대한 정오답 예측을 하는 것이었습니다. 다음 시점의 문항들이란, 2,3,4,5 번째 즉 4개의 문항들이었습니다. 그래서 어텐션 연산을 할 때도 이 2,3,4,5 번째 문항을 Query로 하여 Attention Value를 구했고, 이 4문항에 대한 Attention Value가 FC Network, Sigmoid를 통과해 최종적으로 0과 1사이의 확률값, 즉 2번째 문항을 맞을 확률, 3번째 문항을 맞을 확률, ..., 5번째 문항을 맞을 확률을 뽑게 된 것입니다.
여기까지, 논문에서 지식추적에 어텐션을 적용한 방법을 모두 살펴보았습니다. 머릿속으로만 이해하고 있던 내용을 그림과 함께 표현하니 모호했던 부분들까지 정리될 수 있었는데요. 이 글을 보시는 분들도 조금이나마 이해에 도움이 되었다면 좋겠습니다 😊 또한, 본 글에서는 생략했지만 SAKT 모델 학습을 통해 학습 개념별(Exercise) Attention Weight를 추출해보고 실제로 연관성 있는 개념들에 높은 Score가 추출되는 것을 확인하는 내용까지 논문에 담겨있었습니다. 이 후에 여유가 된다면 해당 실험까지 해본다면 더욱 의미가 있겠네요!
Pytorch로 구현한 SAKT 모델 코드
https://colab.research.google.com/drive/14uP0piSEl8oE2a7lQQWbKm7IxN-yZ8qe?usp=sharing
SAKT_Pytorch.ipynb
Colab notebook
colab.research.google.com
마지막으로 hcnoh 님께서 Pytorch 로 구현하신 코드를 기반으로 코랩위에서 바로 돌려볼 수 있도록 작성해두었습니다. 위에서 논문과 함께 이해해본 글과 비교하며 이해할 수 있도록 글의 인덱스를 주석으로 달아두었으니, 논문 속 수식들과 Layer들이 Pytorch 코드로는 어떻게 구현되고 있는 지를 확인하면 좋을 것 같습니다. :)
