오늘 다뤄볼 추천모델은 Matrix Factorization(이하 MF)입니다. MF는 모델기반 협업필터링의 한 종류로, 유저와 아이템간의 관계를 학습하는 모델입니다. 이 때 유저와 아이템이 가지는 잠재적인 특징을 모델링하게 되고, 이를 Latent Factor Model이라고 부릅니다. MF는 이 Latent Factor Model의 한 종류라고 볼 수 있으며, 아래에서 좀 더 자세히 살펴보겠습니다.
Latent Factor Model
Latent Factor Model 은, 말그대로 잠재 요인 모델입니다.
유저와 아이템의 특성을 벡터(Factor)로 간략화 하는 모델링 기법인데요. 유저와 아이템은 서로 다른 특징을 가지고 있고, 이들이 어떤 관계를 가지는 지를 학습하게 됩니다. 이 때 유저와 아이템을 나타낸 벡터의 길이는 같기 때문에, 같은 벡터 공간안에 표현할 수 있게 됩니다. 아래에서 예시 그림을 살펴보겠습니다.
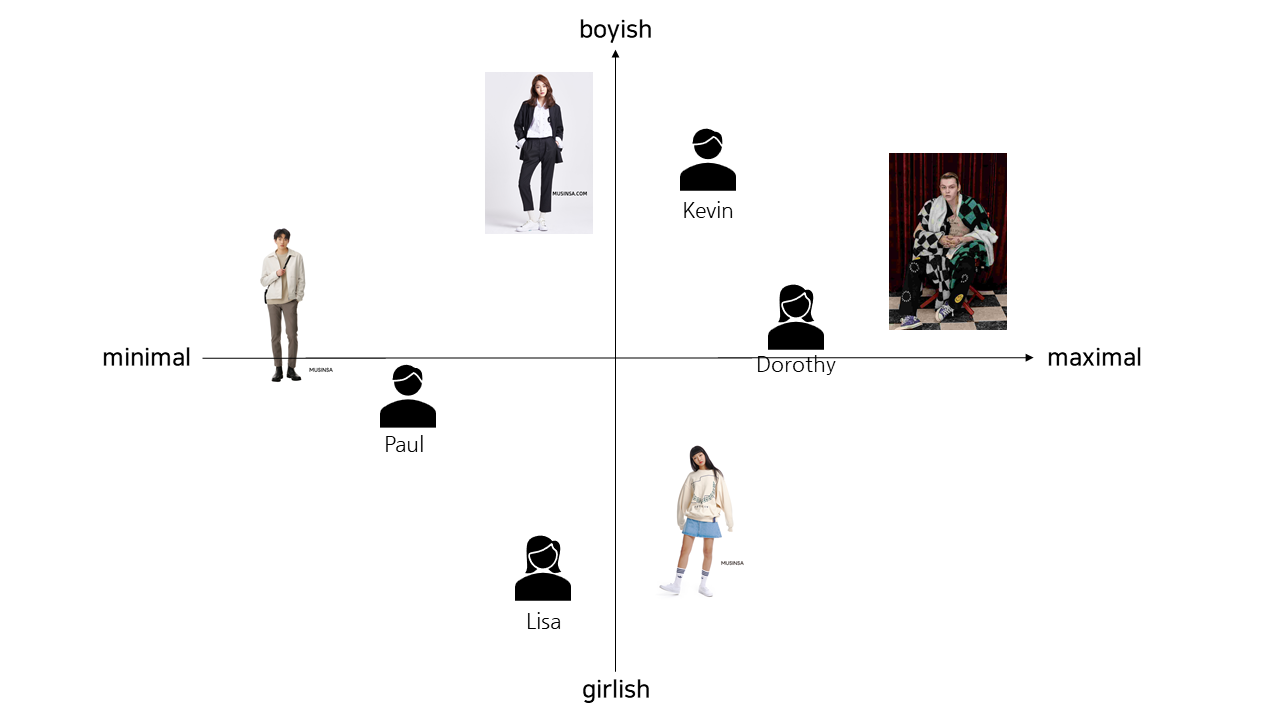
패션플랫폼에서의 유저와 아이템(의류) 의 특성을 파악하기 위해 latent factor를 분석했다고 가정해보겠습니다. 이는 latent factor가 2차원으로 표현된 예시이며, 쉽게 x축, y축 방향으로 각 유저와 아이템(의류)의 벡터 위치가 표현되어 있습니다. 유저와 아이템이 차원이 같은 벡터로 표현되었으므로 이렇게 같은 공간에 표현이 가능하고, 서로의 유사도를 파악할 수가 있게 됩니다.
실제로 Latent Factor Model 은 예시처럼 2차원이 아닌 차원의 수가 정해지지 않은 모르는 차원에 표현될 수 있고, 차원은 여러개일 수 있습니다. 또한, 위 예시처럼 벡터로 명확한 특징을 파악할 수 있는 것은 아닌데요. 말그대로 잠재적 특성을 파악하는것이므로 아이템(혹은 유저)을 표현한 factor는 사람이 명시적으로 이해할 수 없습니다.
그럼 예시로 돌아와서, 위 예시처럼 x축의 양으로 갈수록 맥시멀 패션, y축의 양으로 갈수록 보이쉬한 패션이라는 것은, factor의 공간맵핑을 통해 얻어진 휴리스틱한 판단을 표현한 것 뿐이지 각 차원이 실제로 명시하는 특징은 아닌 것입니다.
Latent Factor Model 를 한줄로 다시 정리하면, 성향을 파악하기 위해 각 유저와 아이템을 잠재 Factor를 표현했고, 이는 같은 공간에 맵핑이 가능하기 때문에 서로의 거리나 각도 등을 통해 유사도를 파악해 잠재적인 취향을 파악할 수 있게 되는 것입니다.
SVD(Singular Value Decomposition)
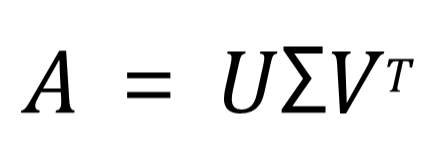
그럼, Latent Factor Model 의 한 종류라 했던 MF 모델을 알아보기 전에, 알아야 할 선형대수 개념이 있습니다. 바로 SVD 라고 하는것인데요. 특이값 분해라고 하는 것입니다.
위 식을 보면, A라는 행렬을 U, S(시그마), V 라는 행렬로 분해하는 것을 확인할 수 있습니다.
U 는 고유값 분해로 얻은 m x m 직교행렬
V 는 고유값 분해로 얻은 n x n 직교행렬
Σ 는 m x n 대각행렬
이때 핵심은 Σ, 바로 시그마 행렬이며, 이 시그마행렬을 이용해서 A를 다시 복원하는 데 사용할 것입니다. 이는 뒤에서 좀 더 자세히 보도록 하고, 어쨌든 이 Σ 행렬은 A의 특징이 담겨져 있는 행렬로, 이 행렬에 대해 양쪽의 U와 V 행렬이 분해되는 것이라 보면 됩니다.
이렇듯 SVD는 행렬을 분해하여, 좀 더 작은 차원의 행렬로 표현하는 기법이기 때문에, 차원축소기법 중 하나입니다.
SVD에는 다양한 종류가 있지만, 이 후 MF를 더 잘 이해하기 위해 Truncated SVD 만 추가로 살펴보겠습니다.
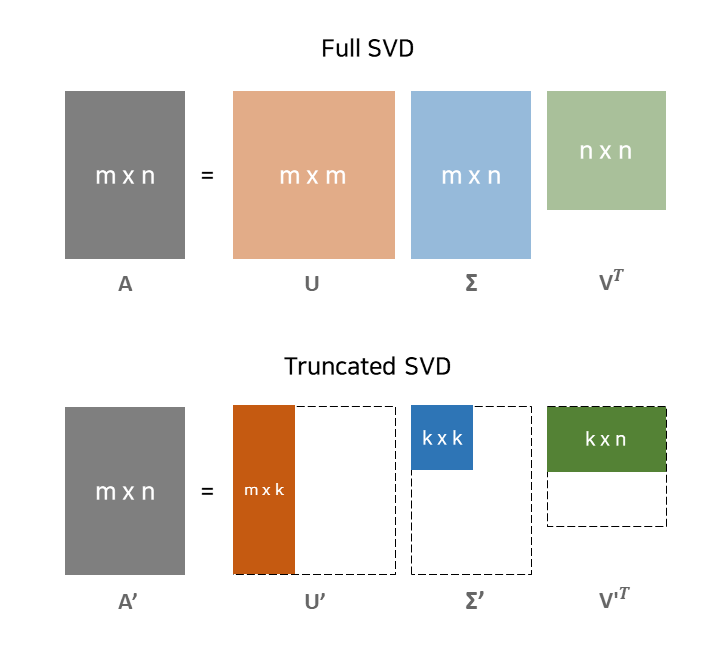
Full SVD는 앞에서 말씀드린 SVD의 기본 형태입니다. m x n 인 A행렬을 U (m x m) * S (m x n) * V(T) (n x n)으로 분해하고 있는데요.
Truncated SVD, 즉 잘린 SVD는 이름 처럼 Σ 를 k x k 크기 만큼만 사용하고 있습니다. 이에 따라 양 옆의 U 와 V 행렬의 모양또한 변형됨을 확인할 수 있습니다.
Σ 는 대각행렬로, 앞에서 부터 중요한 정보를 담고 있는 원소가 정렬되어 있습니다. 이 중 K개의 대각 원소만 사용하더라도, A 의 행렬의 특징을 잘 담는 행렬이라고 보는거죠. 이렇게 k x k 의 크기만 사용하면 당연히 원래 A 행렬을 완전히 표현하지는 못하지만, 이렇게 표현된 A'은 중요한 특징만으로 거의 근사하게 복원된 행렬로써, 좀 더 적은 계산과 좀 더 작은 크기로 표현될 수 있는 특징이 있습니다.
Matrix Factorization
그렇다면, 이 SVD를 사용하여 MF은 어떻게 구현될 수 있을까요? 먼저 MF의 기본 형태부터 살펴보겠습니다.

MF는 Latent Factor Model 이라고 했습니다. Latent Factor Model의 핵심은 유저와 아이템의 잠재 요인을 벡터화 한다는 것이었는데요. 위 그림이 MF의 기본 형태입니다.
추천시스템의 구현을 위해, 유저가 어떤 아이템에 매긴 평가 (Explicit Feedback) 혹은 행동데이터 등 (Implicit Feedback) 이 Sparse Matrix로 표현되어있을 겁니다. 그 행렬을 R이라고 하겠습니다. 이 행렬을 두개의 행렬로 쪼개게 되고, 하나는 User에 대한 Latent Factor가 담긴 행렬, 하나는 Item에 대한 Latent Factor가 담긴 행렬입니다. 그림 속 노란색 행렬 속에 각 유저들에 대한 잠재 벡터가 행방향으로 구성되어 있고, 그림 속 연두색 행렬 속에 각 아이템에 대한 잠재 벡터가 열 방향으로 구성되어있는 형태입니다.
이 때, 각 유저와 각 아이템은 정해진 길이 만큼의 벡터로 정의되고 이 벡터의 길이 K는 직접 정해야 합니다. 행렬의 크기로 MF의 형태를 다시 정리하면, 먼저 m명의 유저와 n명의 아이템 사이의 평점 데이터를 분해하게 됩니다. 이 때 유저와 아이템의 잠재 벡터를 담은 두개의 행렬로 쪼개게 되고, 하나는 m명의 유저에 대한 길이가 k인 벡터가 담긴 m x k 행렬, 하나는 n개의 아이템에 대한 길이 k 벡터가 담긴 k x n 행렬입니다.
MF는 SVD를 통해 구현될 수 있으며, 앞에서 본 Truncated SVD를 통해 좀 더 자세히 뜯어보겠습니다.
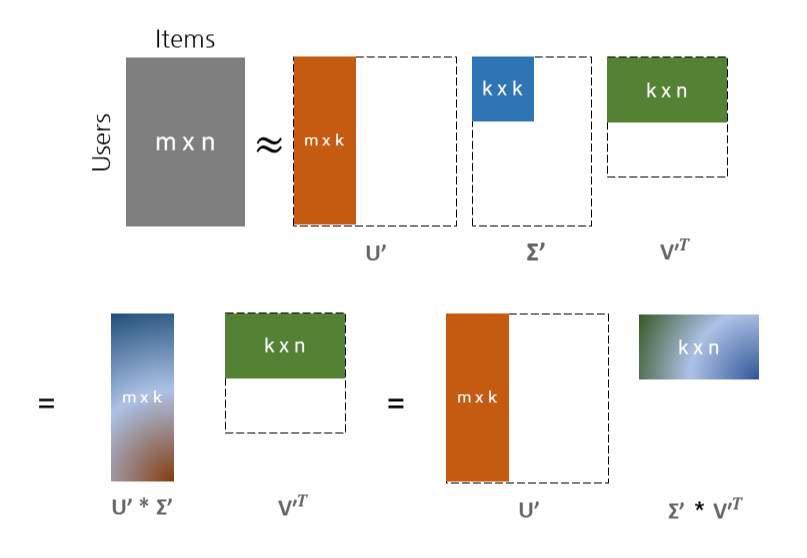
그림과 함께 살펴보겠습니다. Truncated SVD를 통해 우리는 유저와 아이템 간의 sparse matrix를 세개의 행렬로 쪼개 근사하게 표현할 수 있었습니다. 바로 위에 있는 행렬처럼 (m * k), (k * k), (k * n) 의 형태입니다. 그런데 MF는 총 두개의 행렬로 쪼개어 구성되어야 하고, 이는 Truncated SVD를 통해 구현가능합니다.
왼쪽 하단을 먼저 보겠습니다. 주황색으로 표현되었던 m x k 행렬 (U 행렬) 과, 중간의 파란색으로 표현된 k x k (S 행렬) 을 곱하여 m x k 행렬로 만들어주었습니다.
그럼, 오른쪽 하단도 보겠습니다. 이번에는 중간의 시그마 행렬인 k x k 행렬과, 초록색의 k x n 행렬을 곱하여 k x n 행렬을 만들어주었습니다.
어떤 방법을 택하여도 상관없습니다. 둘 중 어떤 것을 사용하더라도 최종 형태는 (m x k) * (k x n) 의 행렬 곱이 만들어지고, 이는 MF의 기본 형태인 유저의 잠재벡터모음 행렬 m x k , 아이템의 잠재벡터모음 행렬 k x n 인 것입니다.
그렇다면, 이렇게 쪼갠 행렬들은 어떻게 사용하는 것일까요? 쪼개었으니, 곱해주면 됩니다. (m x k) * (k x n) 의 곱을 통해 다시 m x n 의 행렬로 복원할 수 있고, 이 복원된 행렬이 예측행렬이 되는 것입니다.
하지만, 유저와 아이템 간의 평점 행렬은 알다시피 Sparse Matrix 입니다. 그럼 이 행렬을 분해하기 위해서는 행렬에 빈공간이 없는 형태여야 하며 빈공간은 보통 0 혹은 평균값 등으로 대체하게됩니다. 이렇게 되면 실제로 관측하지 않은 값에 대해 임의로 판단해버려 모델 성능에 영향을 미칠 수 있게 되고, 이 대신 관측된 값에 대해서만 학습을 할 수 있다면 모델 성능에도 도움이 될 것입니다. MF의 형태를 이해하기 위해 SVD를 살펴보았지만, 실제로 MF는 SGD 등이 Optimization을 통해 학습이 가능하고, 그 과정을 아래에서 살펴보겠습니다.
MF의 학습과정
Objective Function
MF는 모델 기반 협업필터링이며, 유저와 아이템의 잠재 벡터를 "학습" 해야 합니다. 그렇기 때문에 목적함수가 정의되어 있으며, 이를 기반으로 Optimization 과정 또한 거치게 됩니다. 우리가 가지고 있는 유저와 아이템 간의 상호작용을 나타낸 행렬은 Sparse 할 것이며, 이 행렬의 빈공간을 채워나가는, 즉 matrix completion 문제로 정의할 수도 있습니다. 학습을 위해서는 Sparse matrix 안에서 관측된 값들을 가지고 비교해나가며 학습을 하게 됩니다. (SVD만을 사용하여 MF를 구현하면 sparse 행렬의 빈 공간을 평균치나 0으로 대체한 후 행렬분해를 진행하게 되는데, 관측된 값만 가지고 latent vector 를 학습한다면 해당 과정이 필요없습니다.)

학습을 한다는 것은 예측값을 실제값에 가깝도록 잘 예측하기 위해 모델을 조정해나간다는 뜻입니다. 위 수식은 MF 모델의 목적함수(Objective Function) 입니다. X와 Y는 각각 유저의 잠재행렬, 아이템의 잠재행렬입니다. 이 때 실제로 관측된 값(평점)에 대해 학습을 진행하기 위해, 그 위치에서 계산되는 예측평점과 실제평점을 반영해줍니다. 따라서 위 수식에서 시그마 아래에 있는 T는 관측된 유저와 아이템들의 집합이라 볼 수 있습니다.
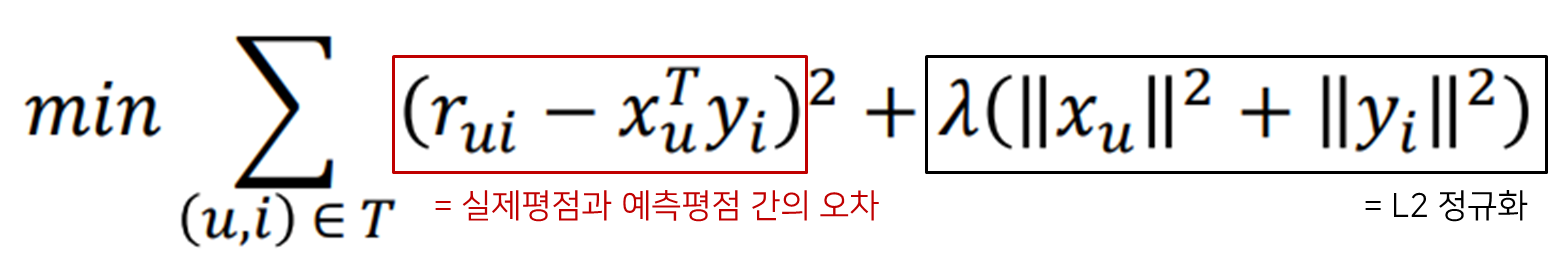
목적함수 수식은 크게 두가지로 구분하여 볼 수 있습니다. 빨간색 박스로 표시한 부분이 실제 평점과 예측평점간의 오차입니다. 이 오차를 제곱하여 더해줍니다. 그리고 오른쪽에 정규화 텀이 추가되어있습니다. 이는 L2 정규화이며, 유저와 아이템 각 행렬이 너무 커지지 않도록 정규화해주고 있습니다. 이 두가지의 식을 모두 더해 최소화(min) 하는 것이 최종 목표이며, 즉 행렬의 크기를 제한해주면서 실제평점과 예측평점간의 오차를 줄여나가는 방향으로 학습해나가게 됩니다.
Optimization
목적함수를 알아보았으니, 이제 본격적으로 학습을 해보겠습니다. 바로 Optimization 과정인데요. MF에서는 대표적으로 SGD 방법을 사용할 수 있으며, 추가로 ALS 방식에 대해서도 알아보도록 하겠습니다.
SGD(Stochastic Gradient Descent)
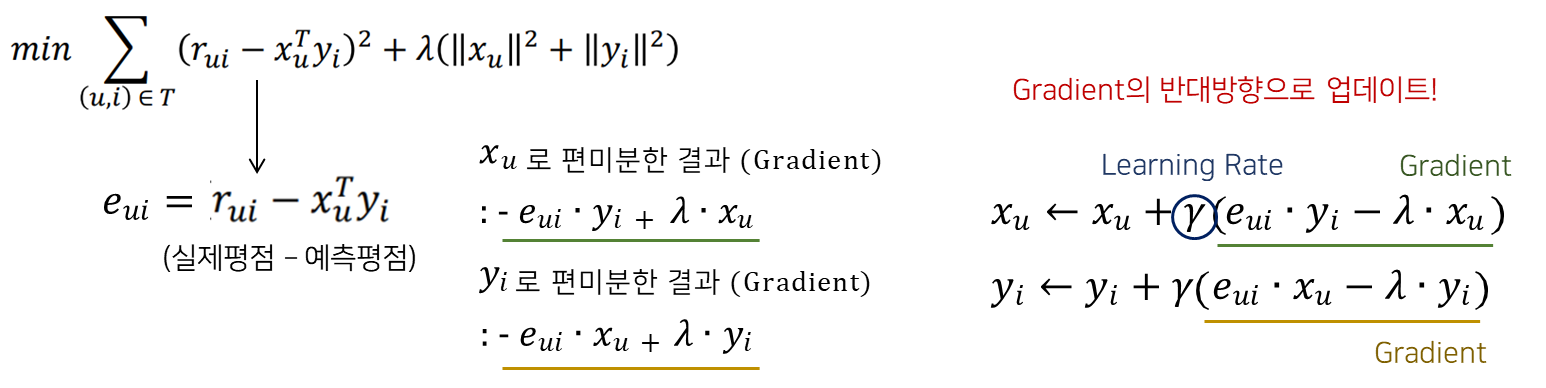
SGD를 위해 먼저 Gradient를 구해주어야 합니다. 위에서 본 목적함수를 유저벡터와 아이템벡터 각각을 기준으로 편미분 해주게됩니다.
유저의 latent vector를 업데이트 해주기 위해서는 현재 latent vector 에서 x_u 로 편미분한 결과(Gradient)를 빼주어 업데이트 합니다. 초록색으로 밑줄을 그은 식이 Gradient에 해당하고 이를 오른쪽 업데이트 식에서 Learning rate를 곱해 빼주었기 때문에 부호가 반대로 변함을 확인할 수 있습니다.
아이템의 latent vector도 동일한 방식으로 진행할 수 있습니다. y_i 를 편미분 하여 해당 Gradient 를 Learning rate와 곱해 현재 아이템의 latent vector에서 빼서 새로운 y_i으로 업데이트 합니다.
위 과정을 실제 예시와 함께 다시 살펴보겠습니다.
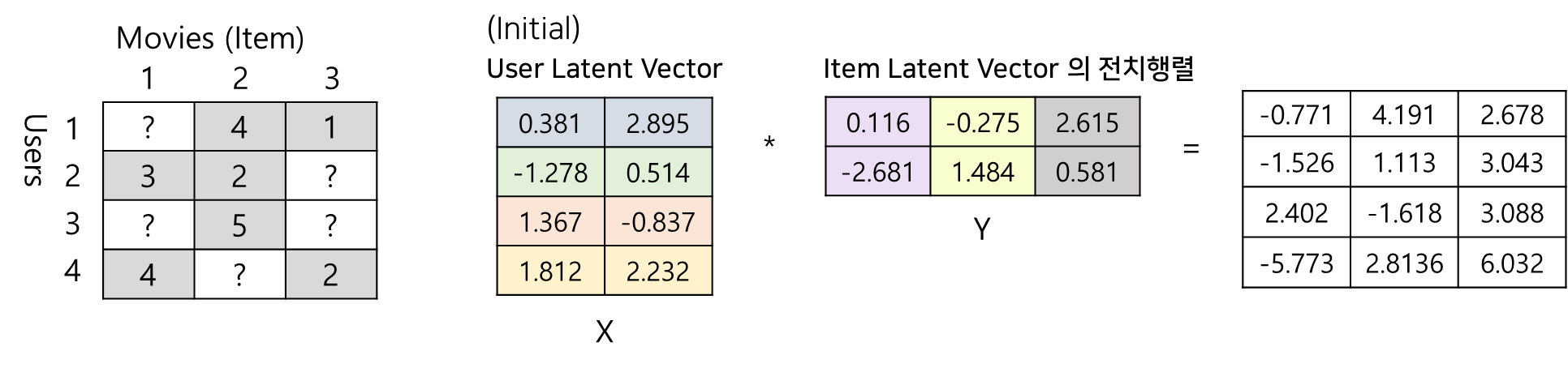
영화를 예시로 들기위해 4명의 유저가 3개의 영화에 대해 매긴 평점데이터를 준비해보았습니다. 유저들이 모든 영화를 보는 것은 아니니, 보시다시피 평가가 내려지지 않은 부분은 물음표로 표시해두었습니다.
먼저, 유저 잠재행렬(User Latent Vector)와 아이템 잠재행렬(Item Latent Vector)를 랜덤으로 초기화한 후 시작해보겠습니다! 그림에서 X가 유저행렬, Y가 아이템행렬이며, 각 유저별로 길이가 2인 잠재벡터들이 4개씩, 각 아이템별로 길이가 2인 잠재벡터 3개가 정의되어 있음을 확인할 수 있습니다. 우리는 이 행렬 두개를 곱해 예측행렬을 도출할 수 있다고 했습니다. 가장 오른쪽에 보이는 것 처럼, X와 Y의 행렬을 곱해 예측평점이 계산된 행렬이 등장했습니다.
그럼, 이 예측행렬과 실제 평점행렬의 오차를 비교해 학습을 해야겠죠!

위 그림은 전 학습과정을 모두 담았습니다. MF의 학습과정에서는 관측된 데이터를 가지고만 학습이 가능하다고 했습니다. 가장 첫번째 순서인 에러를 구하는 과정을 보겠습니다. 1번 유저가 2번영화에 대해 매겼던 4점이라는 "실제평점"과, 예측행렬로부터 나온 "예측평점"간의 오차를 구해주는 과정입니다. 관측되지 않은 1번영화는 건너뛰고, 관측된 영화에 대한 비교를 진행하는 모습입니다.
두번째로, Gradient를 구해야 합니다. 앞에서 유저의 잠재벡터, 아이템의 잠재벡터 각각을 기준으로 목적함수를 편미분해주었으며, 편미분 계산식을 따라 값을 그대로 대입해 계산해주는 과정입니다. 참고로, 람다는 정규화율이고, 임의로 0.01로 정했습니다.
여기서 특히 자세히 보아야 할것은, 현재 우리는 1번유저에 대한 2번영화를 보고 있습니다. 그렇다면 업데이트 해주어야 하는 벡터의 기준또한 1번유저의 잠재벡터, 2번영화의 잠재벡터를 반영해주어야 하며, Gradient 계산시 넣어주는 벡터 또한 y_i는 2번영화의 잠재벡터, x_u는 1번유저에 대한 잠재벡터임을 확인할 수 있습니다.
Gradient를 계산했다면 이를 그대로 학습율(Learning Rate)에 곱해 업데이터 해주고자 하는 벡터에서 빼주면 됩니다. 학습율은 0.1로 진행하였으며, 아래 계산과정에서 확인할 수 있듯, 2번과정에서 구해준 Gradient와 0.1를 곱해 현재 업데이트 하고자 하는 벡터에서 그 값을 빼주고 있습니다. 이렇게 나온 벡터가 업데이트 된 새로운 Latent Vector 이며, 이전 벡터 대신 교체해주면 됩니다.

위 그림 처럼 기존에 1번 유저 위치의 잠재벡터 대신, 새로 업데이트 된 잠재벡터로 교체해주고, 2번영화 위치의 잠재벡터 대신, 새로 업데이트 된 잠재벡터로 교체해주면 됩니다.
이 과정을 모든 관측 평점에 대해 반복해주면 됩니다!
ALS(Alternating Least Squares)
지금까지 SGD를 통한 최적화 과정을 살펴보았습니다. MF에서는 ALS라고 불리는 최적화기법도 적용해볼 수 있는데요. 이는 x_u와 y_i 둘 중 하나를 고정하고 식을 2차식 문제로 풀 수 있는 기법입니다. 이름에서도 알 수 있듯 least square(최소제곱) 문제를 풀게되고, 하나를 고정하고 독립적으로 계산하기 때문에 병렬처리에 사용할 수 있다는 장점이 있습니다.
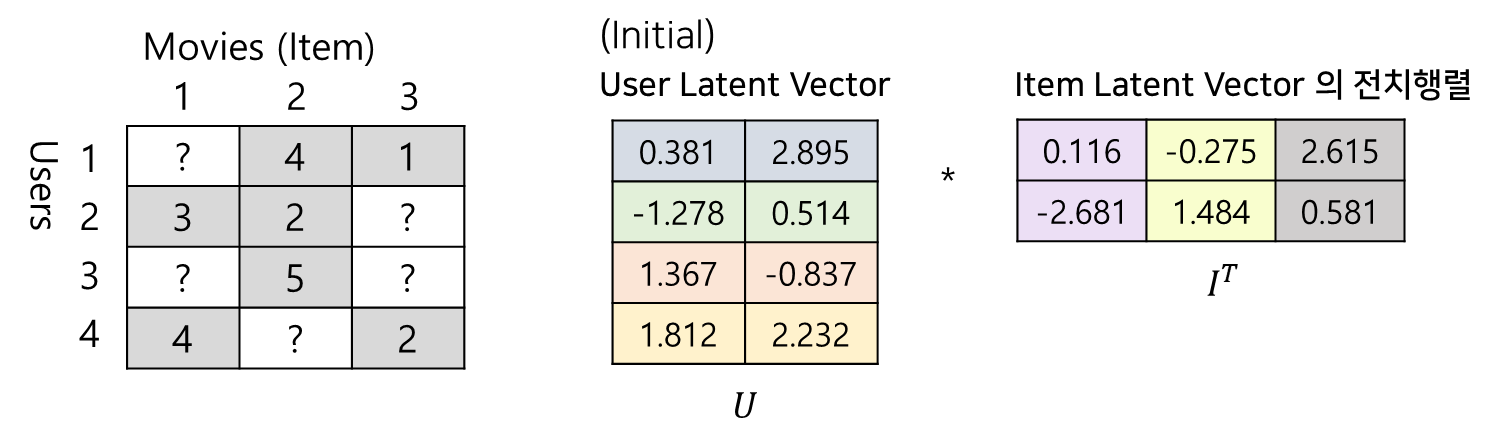
이번에도 SGD 예제에서 사용한 데이터로 예시를 살펴보겠습니다.
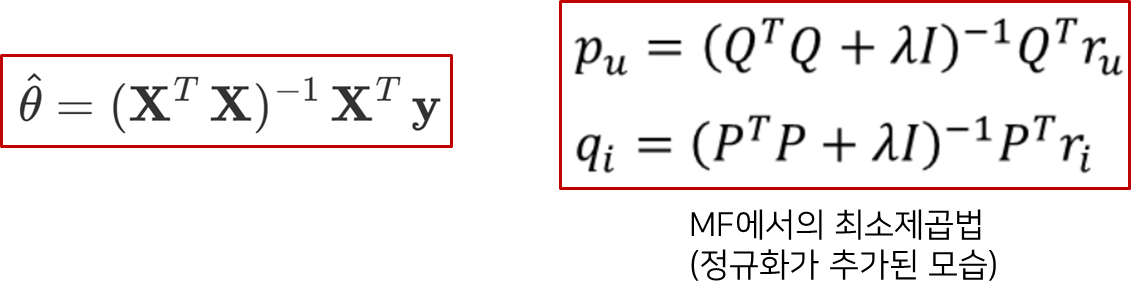
최소제곱법은 선형대수에서 등장하는 개념입니다. 기존 식은 왼쪽처럼, 예측하고자 하는 θ 파라미터는 X, y 와의 식으로 오차가 가장 적은 파라미터를 예측할 수있는 개념입니다. 쉽게 일차함수의 (기울기, y절편)을 구하기 위해 x와 y 값으로 파라미터를 추정하는 과정이라 생각할 수 있습니다. 다시 정리하면, 추정해야할 θ는 X와 곱해졌을 때 y가 나와야 하는 구조입니다.
그렇다면, MF에서는 유저행렬과 아이템행렬을 곱해 평점행렬이 나와야 합니다. 여기서 ALS의 아이디어가 나옵니다.
유저행렬을 예측하고 싶다면 유저행렬을 θ로 두고 X를 아이템행렬, y는 예측해야할 평점행렬로 풀고,
아이템행렬을 예측하고 싶다면 아이템행렬을 θ로 두고 X를 유저행렬, y는 평점행렬로 둘 수 있습니다.
위 그림에서 오른쪽 식이 MF에서 사용되는 최소제곱법으로, X와 y 의 기호표현이 바뀌었고, 정규화식이 추가되었습니다.
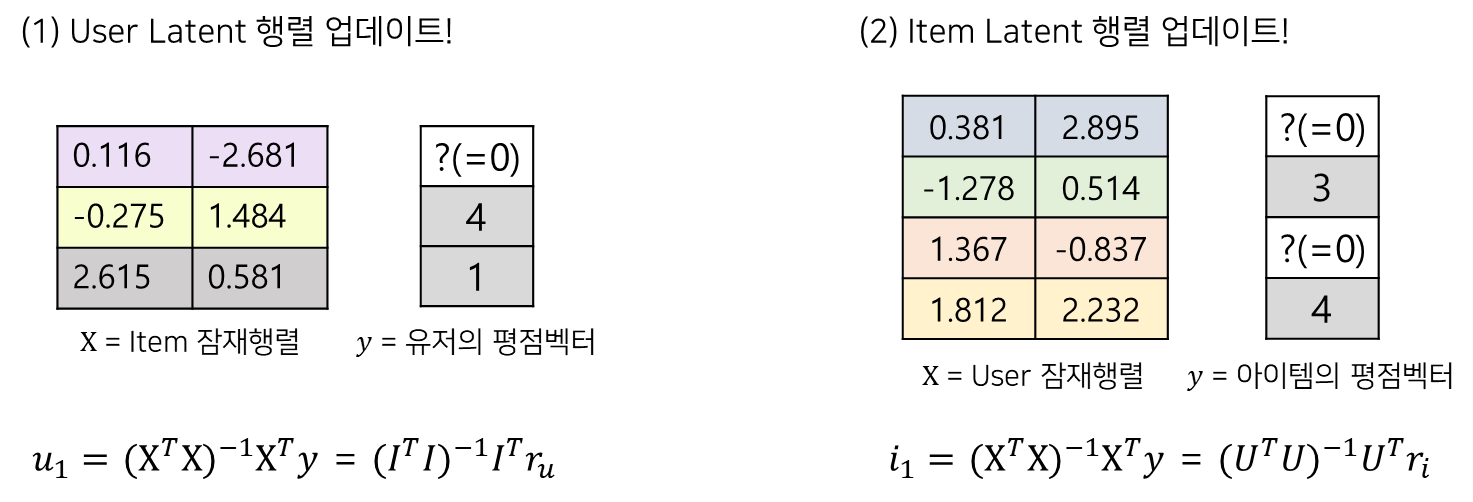
그럼 영화평점예제를 가지고 적용해보겠습니다. 먼저, User 잠재행렬을 업데이트하겠습니다. 위에서 말했듯, User 잠재행렬을 최적의 잠재행렬로 추정하기 위해 θ로 두고, 나머지 Item 잠재행렬을 X, 평점행렬를 Y로 두었습니다. 여러 유저에 대해 병렬처리도 가능하지만, 예시에서는 1번유저의 잠재벡터를 업데이트하기 위해 1번유저의 평점만 스몰 y로 사용했습니다. 아래 식처럼 X 자리에는 아이템 잠재행렬 I, y 자리에는 해당 유저의 평점벡터를 대입하여 계산하면 1번유저에 대한 잠재벡터가 계산되고, 이 과정을 모두 유저에 대해 진행하면 됩니다! 다만, 평점벡터 사용시 행렬계산을 위해 관측이 되지 않은 값에 대해서도 대체값이 필요합니다.
Item 잠재행렬에 대해서도 동일합니다. 이때는 Item 잠재행렬을 θ로 두고, 나머지 User 잠재행렬을 X, 평점행렬를 Y로 두었습니다. User 업데이트 과정과 동일하게 아래 식에 각 행렬 혹은 벡터를 대입하여 계산해주면 끝입니다.
이렇게, Matrix Factorization 의 전반적인 이론을 살펴보았습니다. Latent Factor Model의 개념부터, SVD, MF의 형태 및 학습과정까지 모두 살펴보았는데요. 추천시스템에서 가장 많이 사용되는 모델인 만큼, 머리 속에 잘 정리해야겠습니다. 읽어주셔서 감사합니다!
'AI' 카테고리의 다른 글
| 사용자 PDF 기반 In-context Learning을 통한 ChatGPT 질의응답 챗봇 구현하기 (feat. LangChain, VectorDB) (0) | 2023.06.19 |
|---|---|
| Prompt Engineering 은 어떻게 하는걸까? : ChatGPT 활용 예제와 함께 완벽히 정리하기 (기본편) (1) | 2023.06.18 |
| FM(Factorization Machines)을 활용한 학생별 문항 맞힐확률 예측하기 (0) | 2023.02.26 |
| 시간에 따른 숙련도를 모델링한, DKT(Deep Knowledge Tracing) - 논문정리 및 코드(Pytorch) (0) | 2022.12.30 |
| 협업필터링(CF)을 통해 유사한 학습개념 및 유사한 수준의 학생 찾기 (0) | 2022.12.24 |
